Behind the Equations - 1 ....

Consider the problem: Three filling pipes R, S and T together can fill an empty tank in 2 hours. S can fill the tank four times faster than T. Initially R alone is opened and after x hours, it is closed and immediately S and T are opened. The tank is full after another y hours. If the tank was filled in a total of 4 hours, and x is not equal to y, find the time that T alone would take to fill the tank?

1) 6 hrs 2) 12 hrs 3) 20 hrs 4) 24 hrs 5) 28 hrs

Using equations...

Let R fill the tank in a hours and S and T fill the tank in b and 4b hours. Then we have .

Multiplying throughout by 4ab, we get 4b + 4a + a = 2ab i.e. 4b + 5a = 2ab, (say eqn. 1)

We also have .

Again multiplying throughout by 4ab, we get 4bx + 16a – 4ax + 4a – ax = 4ab i.e. 4bx + 20a – 5ax = 4ab, (say eqn. 2)

Equating the two relations we got, 8b + 10a = 4bx + 20a – 5ax i.e. 4b(2 – x) = 5a(2 – x). Since x is not equal to 2, we can cancel that factor and we get 4b = 5a.

We need to find in how much time will T take to fill the tank i.e. the value of 4b. So substituting 5a = 4b in eqn. 1, we have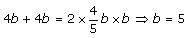

Hence the answer 4b is equal to 20.

There are other ways also to solve this question by equations. Go ahead and solve it by whichever way you have learnt.

The problem with this or other similar approaches is the same issue as mentioned in last post, it’s not very evident what the equation’s mean and specifically when the two equations are equated.

A far more elegant and transparent solution would be as follows...

Since S fills tank four times faster than T, we could consider pipe S as equivalent of 4 pipe T’s. Also since S and T work in tandem, both the pipes together can be taken as equivalent to 5 T’s, let’s say pipe P here onwards.

Now, R and P can together fill the tank in 2 hours i.e. the tank is equivalent to 2 hours of R’s work and 2 hours of P’s work.

If R alone is working for 2 hours and after this, pipe P is working alone for next 2 hours, even then the tank will be full in the 4 hours (since both pipes have done work equivalent to 2 hours).

But in the question it is given that R & P do not work for 2 hours each. Now, understand this carefully...

Say R is working for less than 2 hours, say n hrs less than 2. Thus, it will not fill as much of the tank as it was filling in 2 hours.

Also P would be working for more than 2 hours, in fact for n hours more than 2 hours (since total time has to be 4 hours). And so it will be filling a little more of the tank as compared to what it would have filled in 2 hours.

Even though R fills a little less of the tank and P fills a little more of the tank, the tank is filled. This means whatever less work R has done (in n hours), P has done exactly the same work more (again in n hours).

Thus, pipe R is equivalent to pipe P.

In short,

For whatever time, less/more than 2 hours, R is working ...... P is working for the same time, more/less than 2 hours (since total time to fill is 4 hours)

Also since the tank still gets filled, whatever less/more work is done by R ...... the same amount of more/less work is done by P. In the same time.

Thus, pipe R is equivalent to pipe P.

Since pipe R and P together fill the tank in 2 hours and both are equal, hence each individually will take 4 hours. Thus, pipe P i.e. 5 T’s take 4 hours to fill the tank and T alone will take 20 hours to fill the tank.